To design a first order lowpass Butterworth Filter with cutoff frequency at 6KHz and sampling frequency Fs is 25KHz (i.e. Sampling time = 40us):
SOFTWARE SIMULATION USING MATLAB:
Using “fdatool” toolbox of DSP toolboxes of MATLAB window we can design the filter. Filter parameters like order, cutoff frequency, and sampling frequency are inputted to the “Filter Design & Analysis Tool”. Thus the designed filter has the Filter coefficients as shown below:
Numerator b = [0.5 0.5]
Denominator a = [1 0]
The designed filter is realized using “Filter Realization Wizard” either by opening this toolbox from the “DSP blockset” of ‘Launch Pad’ or by typing “dspfwiz” in ‘Command Window’ and then pressing, “enter” key of the keyboard. Obtained filter coefficients are inputted to the toolbox and the obtained filter model is as shown in Figure (1)
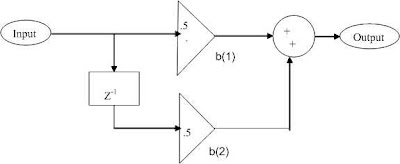
Figure (1)
Simulation of the above filter structure is carried out by the help of “simulink” window, which comprises of “Simulink Library Browser”, “Simulink Debugger” and some other helpful tools.
The input and output block of the above model has to be replaced by ‘Sine Wave’ and combination of ‘Mux’ and ‘Oscilloscope’ respectively by selecting from ‘Simulink Library Browser’ window as shown in Figure (2) below
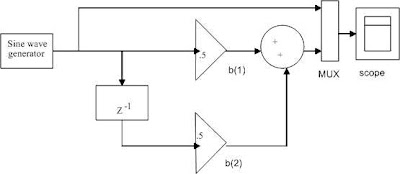
To configure the properties of sine wave generator just double click on that block, which opens an window in which we can write our required input voltage, frequency (in radian) and sampling time (to descritise the signal). Now using ‘Simulink Debugger’ run the model and observe the corresponding output waveform by opening the oscilloscope block.
For different input frequencies the output is studied and it is found that filter is working according to the design.
HARDWARE IMPLEMENTATION:
To implement the digital filter on a digital platform MICROCHIP’s PIC16F877A Microcontroller has been chosen.
Transfer Function Representation: Since numerator and denominator coefficients of the filter are already known, transfer function for the filter can be written as
H (z)=[ 0.5z0+0.5z-1 ] / [ 1z0+0z-೧ ]
We need to convert this transfer function to linear difference equation so that the mathematical equation representation of the digital lowpass filter is implemented by writing a software program for the microcontroller.
In the above transfer function, H (z) is the Z-domain representation of the output signal, z -1 is the delayed sampled input signal. Therefore the above equation can be written as,
y (n)=0.5x(n)+0.5x(n-1)------------------(1)
Or y (n)=1/2[x (n)+x (n-1)]
For n=0, y (0)=0.x (0)+0.5x(n-1)
Assuming x (-1)=0 we have
y (0)=0.5x(0)
Or y (0)=1/2[x (0)]---------------------------(2)
For n=1, y (1)=0.5x(1)+0.5x(0)
Or y (1)=1/2[x (1)+x (0)]-------------------(3)
Interpreting the equation (1) we can find that output y (n) depends on the present sampled input x (n) and previous sampled input x (n-1). For the first sampling time n=0,we can get the first sampled data as zero. Thus we get the equation (2). This equation can be implemented in software. After the next sampling time n=1 we get next sampled data x (1). Also we have the previous sampled data x (0). The obtained equation (3) can also be implemented as a continued part of the software. Now, sufficient amount of initial conditions are available i.e. we have present sampled input value as well as previous sampled input value. Thus computation of the present value of the output requires the knowledge of the present and two previous input samples. Hence, the first two output samples are the result of the assumed zero input sample values at n=1 and n=2 and are therefore the transient part of the output. The steady state is reached at n=2.
Before you get next sampled data x (n)[i.e.x (2)], you make present sampled data x (n-1)[i.e. x (1)] as previous data x (n-2)[i.e. x (0)]. Just sampled input signal i.e. next sampled data is now made as present sampled data x (n-1) (i.e. transfer x (n-1) to x (n-2) and x (n) to x (n-1)). Using the equation (3) itself once again find out the output. This can be easily implemented by looping the equation.
As floating-point arithmetic can’t be implemented directly in PIC Microcontrollers, the floating-point filter coefficients have to be either truncated and/or scaled to a higher value. To accomplish above requirement the equation (1) is multiplied by 2 and rearranged so that we get equation (3).
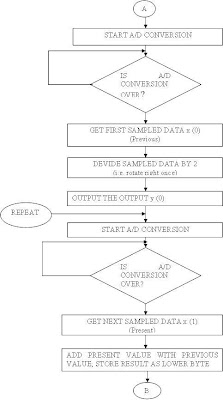
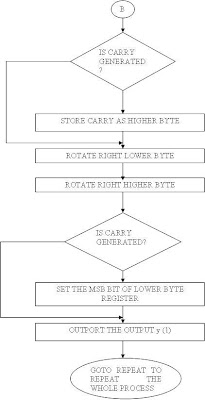
SOFTWARE PROGRAM:
; -------------------------------------------------------------------------------------------
; IMPLEMENTATION OF BUTTERWORTH LOWPASS FILTER
; n=1,Fc=6KHz,Fs=25KHz.
; b=[0.5 0.5]
; a=[1 0]
; y (n)=0.5x(n)+0.5x(n-1)
; or y (n)=1/2[x(n)+x(n-1)]
; -------------------------------------------------------------------------------------------
LIST P=16F877,N=0,ST=OFF, X=OFF
ERRORLEVEL -302
__CONFIG _BODEN_OFF & _CP_OFF & _PWRTE_ON & _WDT_OFF & _WRT_ENABLE_ON & _XT_OSC & _DEBUG_OFF & _CPD_OFF & _LVP_OFF
#INCLUDE
; -------------------------------------------------------------------------------------------
; MACROS TO SELECT REGISTER BANKS
; -------------------------------------------------------------------------------------------
BANK0 MACRO
BCF STATUS, RP0
BCF STATUS, RP1
ENDM
BANK1 MACRO
BSF STATUS, RP0
BCF STATUS, RP1
ENDM
; -------------------------------------------------------------------------------------------
; REGISTER DECLARATIONS
; -------------------------------------------------------------------------------------------
X0 EQU 0X20
X1 EQU 0X21
Y0 EQU 0X22
Y1 EQU 0X24
TEMPLOW EQU 0X26
TEMPHIGH EQU 0X27
; -------------------------------------------------------------------------------------------
; MAIN PROGRAM
; -------------------------------------------------------------------------------------------
ORG 0X0000
START
BANK1 ;select BANK1
MOVLW 0XFF ;enable channel 2 as input
MOVWF TRISA
MOVLW B'10000010' ;configure A/D: right justification,
MOVWF ADCON1 ;A/D conversion clock, select AN2
MOVLW B'10000001'
MOVWF OPTION_REG ;disable pull-up
CLRF TRISC ;Enable PORTC as output
CLRF PIE1 ;Disable peripheral interrupts
CLRF PIE2
CLRF ADRESL ;Clear A/D default destination
; Register
BANK0 ;Select BANK0
MOVLW B'00000001' ;Configure A/D module:ADON,AN2,
MOVWF ADCON0 ;A/D conversion clock, A/D
; Conversion status
CLRF PORTC
; -------------------------------------------------------------------------------------------
;INITIALIZE REGISTERS
; -------------------------------------------------------------------------------------------
CLRF X0 ;Clear declared registers
CLRF X1
CLRF Y0
CLRF Y1
CLRF TEMPLOW
CLRF TEMPHIGH
BCF STATUS, C
CLRF ADRESH
CLRF INTCON ;Disable all interrupt
GOTO MAIN
; -------------------------------------------------------------------------------------------
BSF ADCON0, GO ;Start A/D conversion
NOP ;Wait till conversion is over
NOP
NOP
NOP
NOP
NOP
NOP
NOP
NOP
NOP
NOP
NOP
POLLING1
BTFSC ADCON0, GO ;A/D conversion over?
GOTO POLING1 ;no-check again. yes-continue
BANK1
MOVF ADRESL, W ;Get A/D converted data
BANK0
MOVWF X0 ;First (previous) sampled signal
BANK1
RRF ADRESL, W ;Divide by 2
BANK0
MOVWF PORTC ;Outport first output
REPEAT
BSF ADCON0,2 ;Start A/D conversion
NOP ;Wait till conversion is over
NOP
NOP
NOP
NOP
NOP
NOP
NOP
NOP
NOP
NOP
POLLING2
BTFSC ADCON0,2 ;A/D conversion over?
GOTO POLING2 ;no-check again. yes-continue
BANK1
MOVF ADRESL,W ;get A/D converted data
BANK0
MOVWF X1 ;second (present) sampled signal
MOVF X1,W
ADDWF X0,W ;x(1)+x(0)-->W
MOVWF TEMPLOW
CLRF TEMPHIGH
BTFSC STATUS,C ;is carry generated?
INCF TEMPHIGH,F ;yes-store it
RRF TEMPLOW,F ;divide output y(1) by 2
BCF STATUS,C
RRF TEMPHIGH,F
BTFSC STATUS,C
BSF TEMPLOW,7
MOVF TEMPLOW,W
MOVWF PORTC ;outport output y (1)
MOVF X1,W ;assign X1 (present value) TO X0
MOVWF X0 ;(previous-value)(ie.flushout previous)
CLRF X1
NOP ;to adjust sampling time=40us.
NOP ;i.e. sampling frequency=25KHz
GOTO REPEAT
END
; -------------------------------------------------------------------------------------------
HARDWARE SETUP TO IMPLEMENT THE FILTER:
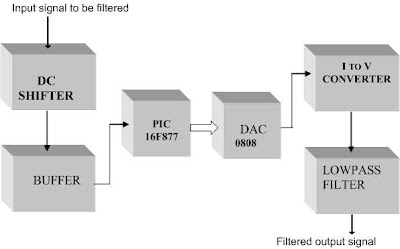
The block diagram of the hardware setup is as shown in the Figure (3). The hardware setup required to implement and test the digital filter is as shown in the Figure (4).
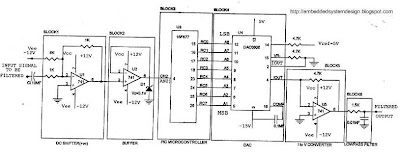
Figure (4)
EXPLANATION FOR THE HARDWARE SETUP:
DC Shifter: - PIC 16F877 doesn’t work for –ve input voltage at all. If a –ve going voltage is applied to the port pin it gets damaged. Therefore it is mandatory to shift the alternating input signal to +ve level completely. This has been achieved using simple opamp inverting adder. The input signal applied is limited to maximum 1v. Hence we need to shift it by just 0.5v towards +ve side. In the DC shifter shown here 2.5v DC shift is provided. Hence even though input increases by mishandling, the whole signal is in +ve DC level itself, by protecting the IC input channel. Care should be taken to see that maximum input swing should not exceed 5v(p-p) otherwise it also damage the IC pins.
Buffer: A simple opamp buffer is connected to avoid the loading effect. It is observed that without a buffer input signal is heavily loaded.
Micro Controller Unit(MCU): Software program is written into MCU, which calculates the output signal for each sampled input signal and outputs it to further processing.
DAC: Digital to Analog Converter (DAC) is used to convert the digital data available from the MCU port pins to analog signal. DAC 0808 is 8bit DAC that gives out the current (see data specification of 0808)
I to V converter: Since the output of the DAC is current this has to be converted to voltage. This is done by simple opamp I to V converter.
RC Lowpass Filter: This is used to smoothen the D/A output signal. RC filter should be designed for cutoff frequency fc=Fs/2 where Fs-->Sampling frequency used to design the filter.
For the above filter let c=0.01uF;f=Fs/2=25KHz/2 =12.5KHz
Therefore, R=1/2.pi.f.c =1/2*3.14*12.5K*0.01u F
=1.326Kohm
Therefore,
Rselected =1.5Kohm
Higher order filters constructed using opamps yield better smoothing results.
FREQUENCY RESPONSE: The frequency response of the digital filter is listed in below table.
Input voltage applied Vi=0.5v
Frequency (Hz) output voltage (volts)
200-------------------------- 2
400 ------------------------- 2
600 ------------------------- 2
800 --------------------------2
1K ---------------------------2
2K ---------------------------2
3K --------------------------1.8
4K --------------------------1.7
5K --------------------------1.6
6K --------------------------1.4
7K --------------------------1.35
8K --------------------------1.3
Graphical response of the above filter is as shown in Figure (5)
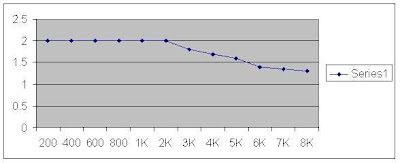
Figure (5)
The response well matches with the designed frequency response. The maximum output voltage remains constant from 0Hz to 2KHz; afterwards it rolls off slowly and for the designed cutoff frequency (i.e. 6KHz) the output falls to 0.707 times of its maximum value. It is appreciable that the designed and observed cutoff frequencies exactly match each other, justifying the fact that as per as the performance is concerned digital filters are always better compared to analog flirters.
CONTROLLING THE SAMPLING FREQUENCY THROUGH SOFTWARE:
Sampling frequency has tremendous effect over filter characteristics. By maintaining filter coefficients constant, if sampling frequency is increased cutoff frequency increases and vice versa. The time gap between two successive switching ‘ON’ of the internal ADC of MCU determines the sampling frequency of the filter. Hence if a particular sampling frequency Fs is chosen for a digital filter, care should be taken so that the processing time doesn’t exceed 1/Fs. This in turn restricts the instruction to be used in a software program. For the PIC 16F877 most of the instruction takes 1us to execute.
If the processing part of the software program takes more time (i.e. more instructions) we have to satisfy with the low sampling frequency (i.e. higher sampling time interval). If higher sampling frequencies are required, instructions to process the signal should be less that in reality difficult to achieve owing to the fixed execution time and limited instruction supported by the microcontroller. This reasons out for the necessity of special hardware devise like specially designed DSP processors to implement the filter at higher frequency ranges.
For the lowpass filter the designed sampling frequency is 25KHz i.e. sampling time interval is 40us. This implies that we should process the signal within 40us. The time interval between switching ‘ON’ of the A/D converter for consecutive 2 times is just 40us. Hence we should write the processing part of the software within 40 execution cycles. This has been achieved in this filter design software.
Consider the software now. Before the loop “go to repeat” starts set a breakpoint. At the end of the loop once again set a breakpoint. Now activating the ‘stopwatch’ from the ‘window’ dropdown list of the MPLAB editor and running the program, gives the total time to go through the loop once. This is found to be less than 40µs .To get required 40µs sampling time interval some ‘NOP’ instructions are added.
Since the sampling frequency is 25KHz the maximum input frequency applicable to the filter is bounded by 12.5KHz.If input signal goes beyond this range “aliasing” of signal will take place and due to this once again the output signal may build up. This is what observed in practice also. When input signal goes above Fs/2 value, output once again increases to certain level and then it starts to diminish and it continuous to happen. Thus to avoid aliasing of the signal sampling frequency should satisfy the Nyquist criteria.
NOISE REJECTION ABILITY OF THE FILTER: -
It is very important for any filter that its noise rejection ability should be as higher as possible. As an example, consider the noise arising from the power lines. This is a usual problem that most of the digital hardware designers face when they design some specific application oriented hardware. In such a problematic situations an accurately designed notch filter centered at 50KHz is used to reject noise generated from the power lines. The center frequency of this filter should be accurate and should have a sharp roll off so that except the noise signal other signal components are passed.
To study the noise rejection capability of the lowpass filter just designed, modified DC shifter circuit, as shown in Figure (6), is used. [For DC shifter circuit refer Figure (4)]
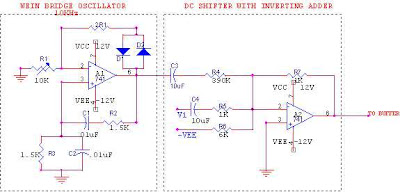
Figure (6)
Opamp Weinbridge oscillator is used to generate 10KHz sinusoidal signal, which is for digital lowpass filter is a ‘noise’ signal. The oscillating frequency of the oscillator is outside the pass frequency of the filter (Remember: cutoff frequency of the filter is 6KHz). This ‘noise signal’ is added with the original input signal to be filtered. Output of the DC shifter is given to subsequent stages as shown in block schematic Figure (3) and Figure (4).
Oscillator output voltage observed is around 15v (p-p). This voltage should be attenuated to applicable microcontroller input voltage limit level. Resistor R4 is used for this purpose (Refer Figure (2.6)). R4 can be varied to get noise signals ranging from some mill volts to equivalent voltage level of original signal.
Signal voltage corrupted by noise voltage level equivalent to signal voltage level results in filtered output with heavy ripples riding over the original signal. Important to note here is even with such high noise signal, at the output side the original signal can be recovered fairly good up to around 3KHz. In practice, however, nowhere we face such a high noise signal rather it may have some mill voltage level only.
To attenuate noise signal use higher values of R4 such as 100Kohm, 220Kohm, and 330Kohm, For R4=390Kohm, the noise signal attenuation is
[1Kohm/390Kohm]*18v = 1*18/390
= 0.04615v
= 46.15mv
Having such a low level noise will not corrupt the original signal much and hence we can easily observe the good reconstructed signal at the output.
When we compare signal to be filtered and filtered signal we find that difference is only small ripples at the output which as mentioned earlier, can be smoothened by using higher order active filters. Nevertheless, at lower pass frequencies R-C lowpass filter itself is sufficient for ordinary applications.
Another noise appears at the output due to the sampling frequency effect. Let signal frequency be 1KHz and sampling frequency is 25KHz. Then total samples per cycle are 25KHz/1KHz=25.Ofcourse, to reconstruct the signal 25 samples are inadequate. However, for study purpose it is fairly enough. Now consider a signal frequency of 6KHz and same sampling frequency. Samples per cycles is given 25KHz/6KHz=4.166 ~ 4. Reconstructing the signal only with 4 samples per cycles is not justifiable. Owing to this reason for around 6KHz onwards noise appears at output. Using higher sampling frequency can solve this problem.
In actual practice, a prealiasing filter is used to reject all noise components which have frequencies above cutoff frequencies so that A/D converter gets only required signal to be filtered. In addition to this prealiasing filter avoids any aliasing effect of the signal.
Unlike analog RC filter, the operation of digital filters doesn’t depend on precise values of the digital signals. As a result a digital circuit is less sensitive to tolerances of component values and is fairly independent of temperature, aging and most other external parameters. Hence noise rejection capability of the filters are considered, digital filters are always superior to analog filters.
References
1. “Digital Signal Processing” By Sanjit K.Mitra
2. “Digital Signal Processing” By P.Ramesh Babu
3. “Digital Filters” By T.J.Terrel And E.T.Powner
4. “BASIC Digital Signal Processing” By Gordon B. Lockart And Barry M.G.Cheetham
5. “Digital Signal Processing” By Alan V.Oppenheim And Ronald W.Schafer
6. “DSP Microprocessors: Advances and Automotive Applications” By Subra Ganeshan And Dr.Gopal Arvamudhan
7. PIC 16F87XA Data Sheet
8. Embedded Control Handbook-1994/95/Microchip
9. Microchip Technical Library CD-ROM-First Edition 2002
10. National Semiconductor CD-ROM-1995/96
11. “Design With PIC Microcontrollers” By John B.Peatman
12. “Opamps And Linear Integrated Circuits” By Ramakant A.Gayakwad
13. “Electronic Principles” By A.P.Malvino
No comments:
Post a Comment
Your Comments... (comments are moderated)