It is often desired to generate various types of waveforms, such as periodic, square waves, sawtooth signals, sinusoids and so on.
A filtering approach to generating such waveforms is to design a filter H (z) whose response h (n) is the waveform one wishes to generate. Then, sending an impulse response d(n) as input will generate the desired waveforms at the output. This type of method is known as “Recursive” method.
In this approach, generating each sample by running the sample-processing algorithm of the filter requires a certain amount of computational overhead. A more efficient approach is to precompute the sample of the waveform, store them in a table in RAM which is usually implemented as a circular buffer and access them from the table whenever needed.
The period or equivalently the fundamental frequency of the generated waveform is controlled either by varying the speed of cycling around the table or by accessing a subset of the table at a fixed speed. This is the principle of so called Wavetable synthesis (lookup table method), which has been used with great success in computer music applications.
Theory of Dual Tone Generation
Generation of a single tone basically implies generating sample of a sine/cosine wave. The z-transform of a sine wave is given as follows:
Z (sine (wt))= Y (z) / X (z) = z.sin (wT) / (z2 –2z cos(wT)+1)
The impulse response of the above transforms (i.e. for x (z)=1) will generate a sine wave of frequency ‘w’ sampled at a rate of T (=1/fs). Thus the above equation is translated to:
y(z) = z-1. Sine (wT) / (1-2z-1cos(wT)+Z-2)
The above equation can be rewritten in a difference equation form as follows:
y (n)-2y(n-1) cos (wT)+y (n-2)=x (n-1) sin (wT)
Rearranging the above equation and setting x (n) as an impulse sequence the following recursive equation are obtained;
y(n) = 2K1y(n-1)-y(n-2)
y(n-2) = y(n-1)
y(n-1) = y(n)
With the following conditions:
K1 = cos(wT)
K3 = initial y(n-2) = 0
For n = 0, y (0) = x (-1) sin (wT)+2y(-1) cos (wT)-y (-2)
=0 -------------------------------------------(1)
(Assuming x (-1) = y (-1) = y (-2) = 0)
For n = 1, y (1) = x (0) sin (wT)+2y(0) cos (wT)-y (-1)
= 1.sin (wT)+2.0.cos (wT)-0
= sin (wT)-------------------------------------(2)
(Since x (0) = impulse input)
For n = 2, y (2) = 0.sin (wT)+2y(1) cos (wT)-y (0)
= 2y(1) cos (wT)-y (0)-----------------------(3)
(Since x (n) = 1 for n = 0
= 0 for else)
Recursive Method of Tone Generation
To generate a tone of frequency f = 50Hz with sampling frequency fs = 500Hz:
Using equation (1) and (2) first find out the initial conditions. Afterwards implement the recursive equation (3). Before the next looping of the equation starts assign present value of output as previous value.
Now let us calculate the values of wT for the above design. Here in this case,
f = 50Hz, fs = 500Hz
\wT = 2pfT = 2*3.14*50*1/500
= 0.62831
\sin (wT) = sin (0.62831) = 0.587785
Similarly, cos (wT) = cos (0.62831) = 0.809016s
The software program written for PIC 16F877 to implement equations (1), (2) and (3) using MPLAB assembler is as follows:
/************************************************************
Filename: tone.c
************************************************************/
#include
#include
main (void)
{
float y0, y1, y2, x; /*variable declaration*/
int i, j;
short int y;
TRISC=0x00; /*set PORTC as out port*/
PORTC=0x00;
y0=0; /*initial value*/
y1=0.587785; /*initial value: sin (wT)*/
for (;;) /*set infinite loop for recursive equation*/
{
/*computation of y2*/
x=2*y1*0.30901;
y2=x-y0;
y=y2*50+50; /* convert float to integer; add fixed DC level*/
PORTC=y; /*out port result*/
y0=y1; /*assign present values to previous value*/
y1=y2;
j=0; /*set delay*/
while (j<22)
{
NOP ();
j++;
} /* End of while loop*/
} /* End of for loop*/
} /*End of main loop*/
/************************************************************/
The above program is written in MPLAB using “HITECH PICC LITE” language tool. When we use this language tool we can write the program in c-code as well as in assembly code. This language tool can be installed by selecting it from the “edit project” option of the ‘project’ menu.
The block diagram of hardware setup to implement the tone generation is as shown below:

Figure (1)
In the block diagram of Figure (1) PIC 16F877 is used to implement the software. Tone generation software is programmed to this microcontroller. Using one of the suitable ports (here PORT C is being used) of the PIC 16F877 the digital tone is out ported to DAC0808. The DAC 0808 converts the generated digital tone to analog format. I to V converter output is given to the DAC to convert the output current of the DAC to voltage. This I to V converted signal is passed through appropriately designed low pass filter to filter out the ripples present on it.
For exact pin-to-pin connection refer figure (2.6b) of chapter 2 wherein same hardware setup is used to implement digital filters. The above hardware setup is valid for both recursive method and Wavetable synthesis method of tone generation.
The above program is programmed to PIC16F877 using PIC universal programmer.
Referring to the equation (3) we can find that computation of y2 will certainly result in floating point +ve and –ve numbers. But as you know outporting floating-point number as well as –ve number in a PIC MCU is not a valid method. Hence we have to convert floating-point number to integer by scaling and truncating and –ve number to +ve number by adding certain amount of DC level. To satisfy both the above requirements y2 is multiplied by an integer 50 and a fixed DC level of 50 is added to this result. This modification we can see in the program ‘tone.c’ on line (24)
To satisfy the sampling time of 2ms (i.e. 1/500) a delay is added. This delay is provided by looping NOP () instruction within while loop. Without this delay the sampling time observed is around 1.66 ms.
Initial conditions y0 and y1 are calculated and directly used in the program. The recursive equation for y2 is implemented by using an infinite ‘for’ loop.
This program yields very good result. The observed frequency of the generated tone is Fobserved=1/Tobserved=1/20ms=50Hz. Since sampling frequency =500Hz and tone frequency is 50HZ, there are total 500/50=10 samples per cycle, which greatly influenced the smoothing of the generated digital tone.
The low pass filter, which is used for smoothing out the ripples of the generated digital tone, is designed for a frequency of 100Hz (i.e. double the tone frequency)
Design: Let R=1.5KW
f=100Hz
Therefore, C= 1/ 2pfR=1/2*3.14*100*1.5*103
=1.0615mF
Since floating-point calculation has to be performed, which usually consumes a lot of time, the maximum sampling frequency achievable is around 600Hz. This limitation is valid only for PIC MCUs with its clock frequency 4MHz. If clock frequency is increased to 20MHz certainly sampling frequency will increase, but not to a very higher value. If higher frequency tone has to be generated then we have to go for either Wavetable synthesis method or use special hardware devices like DSP Processors, which can handle floating-point computations easily and rapidly.
We can generate tones of different frequency or different sampling frequency just by calculating the new value of wT=2pfT and substituting this value in the software.
Wavetable Synthesis (Look up Table) Method of Tone Generation
In this method using equation (1), (2) and (3) we calculate the values of y2 for a cycle or more and we store this data as a table. Each data of the table is accessed with a time delay equivalent to sampling time and out ported continuously. This method yielded very good result compared to recursive method; this method is considered to be a standard method of generating a tone.
Let us generate a tone of 800Hz having sampling frequency of 8000Hz.
wT=2pfT=2*3.14*800/8000
=0.62832
Put this value of wT in equation (1), (2) and (3). From these equations we have to get a table of data, which is descritised representation of sine wave. To get the sine table using above equation we have written a Turbo-c program, which is as follows:
Filename: TONE.C
/************************************************************/
#include
#include
void main()
{
float y0, y1, y2; /*declare variables*/
int i, y;
clrscr();
y0=0; /*initial value*/
y1=sin (0.62832); /*initial value: sin (wT)*/
printf (“\t\t y1=%f”, y1); /*print the value*/
for (i=0;i<=20;i++); /*set finite loop*/
{
y2=(2*y1*cos (0.62832)-y0); /*compute y2*/
y=(y2*50)+50; /*scaling and dc shift*/
printf (“\t\t y=%d”, y); /*print the value*/
y0=y1; /*assign present values to previous value*/
y1=y2;
} /*end of for loop*/
getch();
} /*end of main*/
/************************************************************/
The obtained table data are:
[97,97,79,49,20,2,2,20,50,79,97,97,79,49,20,2,2,20,50,79,97]
Looking into the table we can observe that it contain descritised values of sine wave of more than one cycle. Now we have to check 2 things. One: whether above table data resembles a sine wave? Two: whether this table data corresponds to a frequency of 800Hz?
To solve first question use “chart wizard” option of Microsoft Excel. Using Microsoft excel we can draw the graphical representation of above obtained list of values and we can check whether it resembles the sinusoidal signal shape.
Write obtained values of the table in any column. Select the column using left button of the mouse. Click on “chart wizard” icon of toolbar. Chart wizard opens up. Select: Standard Types®Chart type® Line® Chart sub-type and click “next” press button. The plot of the all-21 values corresponding to each sampling time is displayed as shown in Figure (2). Here we can observe the sinusoidal format of the obtained values.

Figure (2)
Now to check whether table data contains our required frequency signal we have to find the frequency spectrum of the table data. For this a MATLAB M-file program is written and 'fft' (Fast Fourier Transform) of the table data is computed and plotted according to the scale. The program is shown below:
/******************************************************
File name: dtmf.m
******************************************************/
t=0:0.0001:0.8; % set time scale
y=[97,97,79,49,20,2,2,20,50,79,97,79,49,20,2,2,20,50,79,97]; %tone table
y1=fft (y, 512); %find fft
Pyy=y1. *conj (y1)/512; %find power spectrum
f=8000*(0:256)/512; %set appropriate scale
plot (f, Pyy (1:257)); %plot the response
grid; %show grid lines
title (‘Frequency Content of y’);
xlabel (‘Frequency (Hz)’);
ylabel (‘Magnitude’);
/*******************************************************/
The frequency spectrum obtained from the above program is as shown below in Figure (3).
In frequency spectrum we can observe two peaks: one is at 800Hz, which corresponds to the frequency of the tone, and another peak is at 0Hz, which corresponds to the fixed added DC level.
Thus through software methods we have confirmed that the Wavetable (lookup table) has all required characteristics as we have designed. Now to observe the tone in reality let us write MPLAB program so that the program can be implemented on PIC MCU.
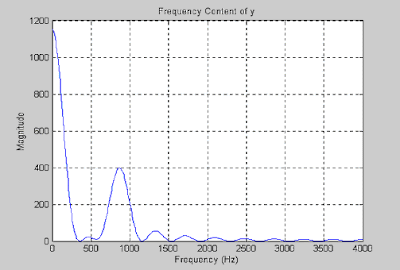
Figure (3)
/***********************************************************
File name: tone1.c
***********************************************************/
# include
#include
main(void)
{ /*declare tone table, variable*/
int a [21]={97,97,79,49,20,2,2,20,50,79,97,79,49,20,2,2,20,50,79,97}, i;
TRISC=0x00; /*set PORTC as out port*/
PORTC=0x00;
While (1) /*set infinite loop*/
{ /*set finite loop*/
for (i=0;i<=20;i++)
{
PORTC=a [i]; /*out port the result*/
j=0;
While (j<4) /*set delay*/
{
NOP ();
j++;
} /*end of while loop*/
} /*end of for loop*/
} /*end of while loop*/
} /*end of main*/
/**********************************************************/
This program exactly delivers the sine wave of 800Hz as we have seen in MS-Excel plot in Figure (2). To adjust the sampling frequency of 1/8000=125ms a delay loop is added.
Same above Wavetable can be used to generate tones of different frequency. If the delay is made zero then, whatever the frequency we observe, is the maximum attainable frequency with PIC MCU having 4MHz clock frequency. If the delay time is varied, sampling time also varies which in turn vary the frequency of the generated tone. As delay is increased, sampling time goes on increasing that in turn decreases sampling frequency causing corresponding decrease of frequency of generated tone.
Dual Tone Generation
To generate dual tone we use lookup table method as it gives nice result. To do this first we should generate two single tones and add these two tones together and then if necessary scale the result.
Let us generate a dual tone having 2 frequency contents f1=800Hz and f2=1100Hz being sampled regularly with sampling frequency 8000Hz.
For tone1: wT=2*pi*f1*T
=2*3.14*800*1/8000
=0.62832
For tone2: wT=2*pi*f2*T
=2*3.14*1100*1/8000
=0.8639
To get Wavetable for the tone1 substitute the value of wT=0.62832 in Turbo-c program TONE.C and run the program.
Obtained wave table is,
tone1=[97,97,79,49,20,2,2,20,50,79,97,97,79,49,20,2,2,20,50,79,97]
To get Wavetable for the tone2, substitute the value of wT=0.8639 in Turbo-c program
TONE.C. Obtained Wavetable is,
tone2=[99,76,34,3,5,38,79,99,85,46,9,1,27,69,97,92,57,17,0,17,57]
Both above tones can be checked for its shape and frequency contents as we have done in explaining Wavetable method. Here we will not do this, as it would be mere repetition of what we have done earlier.
To get dual tone add tone1 and tone2 wave tables. The resultant dual tone table is,
tone1+tone2=[196,173,113,52,25,40,81,119,135,125,106,98,106,118,117,94,59,37,50,96, 154]
This dual tone table as it is will not deliver satisfactory result. It is because; remember that tone1 and tone2 are added with same fixed DC level. When you add tone1 and tone2 this DC level also gets added up. Because of this reason the value reaches to either saturation or cutoff level and hence we will end up with a square wave instead of sine wave.
To overcome the problems divide the each data of the dual tone table by 2. The resultant table is,
tone1+tone2/2=Dual tone
=[98,87,57,26,13,20,41,60,68,63,53,49,53,59,59,47,30,19,25,48,77]
In this computation, we get fractional part. These fractions are rounded to nearest integer.
To see how this dual tone looks like, use MS-Excel as mentioned earlier. Thus the plotted graph for dual tone table is as shown in Figure (4).

Figure (4)
Using dtmf.m program we can find out the frequency spectrum of the dual tone. For this replace the value of y by dual tone table given above and change the title to ‘Dual Tone Spectrum: f1=800Hz & f2=1100Hz’. Thus observed frequency spectrum is as shown in Figure (5).

Figure (5)
From the frequency spectrum, we can observe 3 peaks: one corresponding to DC level (0Hz), other one is for 800Hz and another one is for 1100Hz. But these peaks are not exactly located over 800Hz and 1100Hz. There is a slight shift of these frequencies over frequency range. This happened due to the error introduced when we have performed truncation and scaling of the Wavetable data.
To implement the dual tone on hardware, substitute dual tone table as a[i] in program tone1.c and program the tone1.hex file to PIC16F877 IC.
The observed dual tone on CRO exactly resembles the waveform that we have got with MS Excel plot.
In the above program delay is adjusted to get a sampling time of 125ms(i.e. sampling frequency 8000Hz)
For the low pass filter, design is as follows:
Let f =2200Hz,
R=1.5KW
Therefore, C = 1/2pfR = 1/(2*3.14*2200*1.5*103 )
= 4.82532mF
In the program tone1.c without any delay loops minimum sampling time achievable (for PIC MCUs with clock frequency 4mHz) is 25ms i.e. maximum sampling frequency is 1/25ms=40KHz. This means that we can generate a dual tone, which can contain a tone of around maximum 10 KHz frequency.
The extended part of the dual tone generation is the generation of “Dual Tone Multi Frequency (DTMF)” signal, which are widely used in modern telecommunication field.
Applications of Dual Tone
Tone generation is required in many applications. It can be used in applications involving secure off-site control, where commands or data in the format of tones are transmitted over a telephone tone. The tone generation finds application involving signal modulation as well. The routine can be used to generate audible tones and output for speaker connected to an I/O port or a PWM channel. Dual tones are heavily used in DTMF signal generation.
Your blog is too help full. But fig (2.6b) is not there.Please upload the figure
ReplyDeleteVery nice, thank you
ReplyDelete