Filter parameter: Fs=10KHz i.e. sampling time =1/10
=100us.
Fc = 2KHz
Apass = 1dB
Order n = 2
SOFTWARE SIMULATION: - The above filter is designed and simulated using “fdatool”, “simulink” and “dspfwiz” as explained in the earlier section.
HARDWARE IMPLEMENTATION: - To implement the filter in hardware we need to have a transfer function and its corresponding linear difference equation representation of the filter.
From the “fdatool” the obtained numerator and denominator coefficients are as follows,
Numerator b = 0.21797
0.43596
0.21798
Denominator a = 1.0000
-0.35135
0.32966
Since the PIC 16F877 Microcontroller does not directly support floating-point arithmetic, the numerator and denominator coefficients are equivalently converted to integer values by truncating and scaling by a factor of 4, which yields the filter coefficients as
b = [1, 2, 1]
a = [4, -1, 1].
Therefore,
Transfer function of the filter is,
H (z) = [ 1 + 2Z-1 + Z-2 ] / [4 - Z-1 + Z-2 ]
Converting the transfer function to linear difference equation we can write,
4y(n) – y (n-1) + y (n-2) = x (n) + 2x (n-1) + x (n-2)
Or y (n) = 1/4 [x (n) + 2x (n-1) + x (n-2) +y (n-1) – y (n-2)]
For n=0, y (0)=1/4[x (0)];
[Assuming the initial condition that x (-1), x (-2), y (-1) and y (-2) are zero].
For n=1, y (1)=1/4[x (1)+2x(0)-y (0)]
For n=2, y (2)=1/4[x (2)+2x(1)+x (0)+y (1)-y (0)]
Where x (0), x (1) and x (2) represents sampled values of input signal, y (0), y (1) and y(2) represents filtered output values.
FLOWCHART OF THE SOFTWARE: -

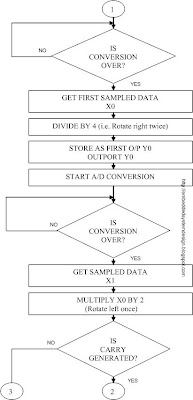




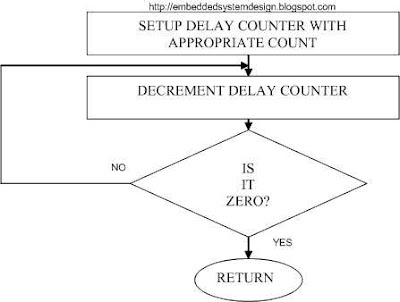
DELAY SUBROUTINE FLOWCHART:
HARDWARE SETUP: -The hardware setup for this filter implementation remains unchanged as shown in earlier blog post. Only change that we have is the design of RC lowpass filter.
Design:
Fc=Fs/2=5KHz; Let R=1.5KW.
Therefore,
C= 1/2*p*fc*R = 1/2*p*5K*1.5K=21.22nF
Therefore,
C selected=22nF
FREQUENCY RESPONSE: - The observed frequency response of the filter is as listed below,
Input voltage Vi=0.5v
Input Frequency (Hz) Output voltage (volts)
100----------5
200-----------5
400----------- 5
600----------- 5
800----------- 5
1K --------- --5
1.2K----------5
1.4K----------5
1.5K----------4.6
1.6K-----------4.5
1.8K---------- 4.0
1.9K-----------3.8
2.0K-----------3.5
2.1K-----------3.2
2.2K-----------3.0
2.4K-----------2.5
2.6K-----------2.0
2.8K-----------1.5
3K -----------1.0

Figure (1)
The magnitude corresponding to 3dB frequency is 5*0.707=3.535v. Note that the observed cutoff frequency is 2KHz, which is same as that of theoretically designed (In the frequency response list shown above shows 3.5v at cutoff frequency. In fact the value is 3.53 itself. But since on a CRO reading accuracy is limited by the ranging of voltage and error in reading the data, we have written the voltage value as 3.5; remember that it is not because the filter doesn’t exhibit exact cutoff frequency but we can’t read the response accurately).
2.4.6.SAMPLING FREQUENCY OF THE FILTER: - Sampling Frequency of the filter designed is 10KHz which implies that sampling time =1/10K=100ms.
Hence the looping part of the software should be completed within 100ms and has been achieved with just 83ms. To satisfy 100ms sampling time, delay is used. At the very beginning of the filter response there may be transient due to unsatisfied condition of sampling time and initial condition.
The discussion carried over the effect of sampling frequency variation and aliasing effect in earlier section also hold good here.
NOISE REJECTION ABILITY OF THE FILTER: - To study this, hardware setup is constructed as it is been constructed for I order Butterworth lowpass filter implementation.
Now our importance shifts to do a comparison of noise rejection capability of the I order and II order filter. There can’t be a second opinion about the performance of II order filter in eliminating the noise and thus making the signal ‘smoother’. Now our attention is drawn towards to have a trade-off between the performances of the filters.
Second order filters have sharper cutoff compared to first order filters, which is observed in this filter also. As per as noise is concerned both filters perform well.
LIMITATIONS: -
PIC Microcontrollers impose a lot of limitations in implementation of digital filters. Reader might be remembering that PIC MCU’s are 8-bit controllers having “Harvard Architecture” as its internal architecture. Those who wishes to study the digital filter response using PIC using PIC MCU’s as a tool are suggested to take notice of mentioned obstacles:
Processing of A/D converted data: - PIC 16F877 has a 10-bit built in internal ADC. The A/D converted data are stored in two 8-bit registers called ADRESL and ADRESH. The lower byte is stored in ADRESL and the remaining two higher bits are stored in ADRESH. Now the problem is, since to process this 10-bit A/D data it requires having 16-bit arithmetic operation, implementation, which in PIC 8-bit MCU, is a cumbersome job.
To overcome this problem care is taken when applying the input signal so that A/D converted data doesn’t exceed 8-bit or even it exceeds it should exceed the value by one bit only. All A/D converted bits are high when input is 5V.When input voltage is around 2.5V only lower bits of the A/D converted data are high. This is been tested by directly displaying the A/D converted data.
Now referring to DC shifter circuit in Figure (2.6b), the DC shift provided by the circuit is = -(1K W/6K W)*(VEE)
= -(1/6)*(-12V)
= 2V
But maximum input voltage level that can be applicable to get 8 bit A/D converted data is 2.5V
Therefore,
The voltage swing that can be applicable =2.5V-2V
= 0.5V
Thus the input signal to the PIC port pins can vary from 1.5V to 2.5V, 2V being DC value. Therefore for DC shifter, since there is already 2V DC shift provided by DC shifter, the maximum applicable input voltage is 1V.This is the reason why we have applied only 0.5 V input signal. If input level to DC shifter circuit exceeds 1V A/D converted data will exceed 8-bits which is processed by the software and hence even though the filter work according to the design, signal loses its original shape.
Sampling frequency limitation: - The time taken to complete single loop in final looping port of the software determines the sampling time. The first order Butterworth lowpass filter designed in our study used sampling frequency 0f 25KHz which implies sampling time = 40ms. Software routine written for any other, same or higher order filter utilize more than 40ms for its looping part. Hence with 4MHz clock frequency for the operation of PIC MCU, the maximum possible sampling frequency is 25KHz. Thus to get fairly good filtered and reconstructed signal, the maximum input signal frequency is applicable is around 10KHz. If higher clock frequency like 20MHz is used the A/D conversion speed is more. This saves time and hence sampling frequency can be higher to a little bit.
Floating-point arithmetic and –ve results: - Another major drawback of the PIC MCU is it doesn’t support floating-point arithmetic operations, which are very crucial aspects when we deal with digital filters. Owing to this reason floating point filter coefficients are truncated as well as scaled to an integer when we did this precautions are taken so that filter response does not change considerably beyond required designed response.
Truncated and scaled filter coefficients of lowpass filter have not much affected the filter characteristics. But for high pass and band pass/reject filters in addition to floating point arithmetic problems, -ve numbers also came into picture; processing of these –ve numbers and D/A conversion becomes another difficult job. Somehow floating point numbers can be handled, but playing with –ve numbers is certainly a tedious job.
The above floating problem can be overcome by using ‘PICLITE’ assembler, which is supported by MPLAB. By enabling the ‘PICLITE’ assembler we can write the program in C code as well as in assembly code. C codes are converted to assembly code by the assembler itself. These assembled codes can be programmed to PIC MCU.
References
1. “Digital Signal Processing” By Sanjit K.Mitra
2. “Digital Signal Processing” By P.Ramesh Babu
3. “Digital Filters” By T.J.Terrel and E.T.Powner
4. “BASIC Digital Signal Processing” By Gordon B. Lockart And Barry M.G.Cheetham
5. “Digital Signal Processing” By Alan V.Oppenheim And Ronald W.Schafer
6. “DSP Microprocessors: Advances and Automotive Applications” By Subra Ganeshan and Dr.Gopal Arvamudhan
7. PIC 16F87XA Data Sheet
8. Embedded Control Handbook-1994/95/Microchip
9. Microchip Technical Library CD-ROM-First Edition 2002
10. National Semiconductor CD-ROM-1995/96
11. “Design with PIC Microcontrollers” By John B.Peatman
12. “Opamps and Linear Integrated Circuits” By Ramakant A.Gayakwad
13. “Electronic Principles” By A.P.Malvino
No comments:
Post a Comment
Your Comments... (comments are moderated)